Multi-Pitch Spectrum in Log-Frequency domain

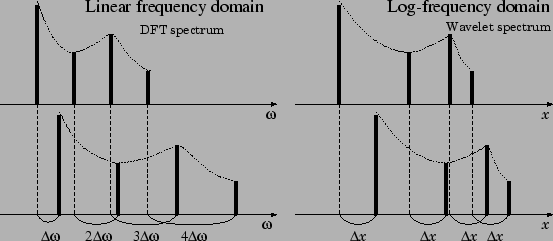
First, we discuss a single-tone signal with a single fundamental frequency and a harmonic structure. In the linear frequency scale, frequencies of 2nd harmonic, 3rd harmonic, $\cdots$, $n$th harmonic are integral-number multiples of the fundamental frequency. This means if the fundamental frequency fluctuates by $\Delta\omega$, the $n$-th harmonic frequency fluctuates by $n\Delta\omega$. On the other hand, in the logarithmic frequency (log-frequency) scale, the harmonic frequencies are located $\log 2,$ $\log 3,$ $\cdots,$ $\log n$ away from the log-fundamental frequency, and the relative-location relation remains constant no matter how fundamental frequency fluctuates and is an overall parallel shift depending on the fluctuation degree (see Fig 1).

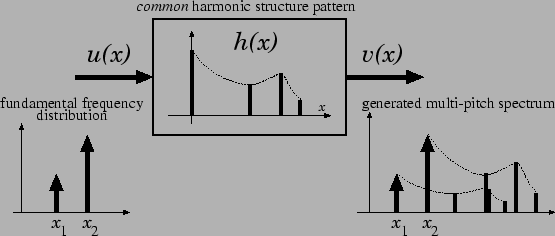
Let us assume that all single-tone signals have a common harmonic structure which does not depend on the fundamental frequency. We call it the common harmonic structure and denote it as $h(x)$, where $x$ represents the logarithmic frequency. The fundamental frequency position of this pattern is set to the origin (see Fig 2). Obviously, this assumption is not true for real music sounds, but is practically approximate in many cases as shown later.

Next, we define a function $u(x)$ to represent the distribution of fundamental frequencies in a multipitch signal. If $u(x)$ is simply an impulse function, for instance, it represents the logarithmic fundamental frequency and the power of the single tone with a harmonic structure $h(x)$.

If we assume that the power spectrum is additive¹, the power spectrum of a multipitch signal is represented as a convolution of the fundamental frequency distribution $u(x)$ and the common harmonic structure $h(x)$:

$$v(x)=h(x)*u(x)$$ (1)

as shown in Fig 2. In other words, the power spectrum $v(x)$ of a multipitch signal can be regarded as the output of a filter $h(x)$ representing the common harmonic structure given the input $u(x)$ representing the fundamental frequency distribution. This relation can be extended to non-harmonic and/or continuous spectrum $h(x)$ and continuous distribution $u(x)$ if the single-tone spectrum is log-frequency shift-invariant and power spectrum is additive.

図 1: Relative location of fundamental frequency and harmonic frequencies in linear and logarithmic scales.

図 2: Multi-pitch spectrum generated by convolution of fundamental frequency pattern and the common harmonic structure pattern.