


�$B Another Interpretation as Clustering
�$B>e$X�(B: A Maximum Likelihood Formulation
�$BLa$k�(B: Model of Harmonic Structures
Model Parameter Estimation using EM Algorithm
Since the observed spectral density function 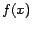 , where
, where 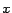 denotes
log-frequency, is considered to be
generated from the model of multiple harmonic structures, the log-likelihood difference
in accordance with an update of the model
parameter
denotes
log-frequency, is considered to be
generated from the model of multiple harmonic structures, the log-likelihood difference
in accordance with an update of the model
parameter
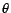 to
to
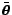 is
is
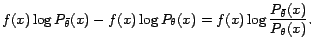 |
|
|
(2) |
Although Dempster formulated EM algorithm [8] in order to maximize the mean
log-likelihood considering 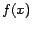 as a probabilistic density function,
it can also be formulated in a same way even if
as a probabilistic density function,
it can also be formulated in a same way even if 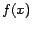 is replaced with
spectral density function.
By taking expectation of both sides with respect to
is replaced with
spectral density function.
By taking expectation of both sides with respect to
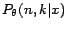 which represents the probability of the
which represents the probability of the 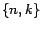 -labeled Gaussian
distribution from which
-labeled Gaussian
distribution from which 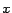 is generated,
is generated, 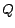 -function will be derived
in the right-hand side.
Given
-function will be derived
in the right-hand side.
Given 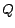 -function as
-function as
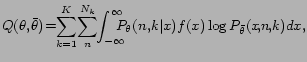 |
|
|
(3) |
thus it yields
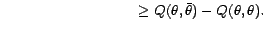 |
|
|
(4) |
By obtaining
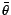 which maximizes the
which maximizes the 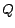 function, the log-likelihood of the model of multiple harmonic structures with
respect to every
function, the log-likelihood of the model of multiple harmonic structures with
respect to every 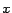 will be monotonously increased. A posteriori
probability
will be monotonously increased. A posteriori
probability
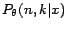 in equation (3) is given as
in equation (3) is given as
where
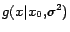 is a Gaussian distribution.
By the iterative procedure of the two steps as follows,
the model parameter
is a Gaussian distribution.
By the iterative procedure of the two steps as follows,
the model parameter
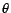 locally converges to ML estimates.
locally converges to ML estimates.
Initial-step
Initialize the model parameter
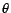 .
.
Expectaion-step
Calculate
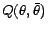 with equation (3).
with equation (3).
Maximization-step
Maximize
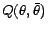 to obtain the next estimate
to obtain the next estimate
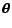 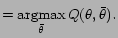 |
|
|
(8) |
Replace
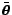 with
with
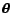 and repeat from the Expectation-step.
and repeat from the Expectation-step.



�$B Another Interpretation as Clustering
�$B>e$X�(B: A Maximum Likelihood Formulation
�$BLa$k�(B: Model of Harmonic Structures
�$BJ?@.�(B16�$BG/�(B3�$B7n�(B25�$BF|�(B
.
Maximization-stepwith equation (3).
to obtain the next estimate
with
and repeat from the Expectation-step.