
 齊藤翔一郎 ,
齊藤翔一郎 ,  亀岡弘和,
亀岡弘和,  高橋佳吾 ,
高橋佳吾 ,  小野順貴 ,
小野順貴 ,  西本卓也 ,
西本卓也 ,  嵯峨山茂樹
嵯峨山茂樹 【目的と概要】レコードやCDの楽曲を楽譜に起こすという古くから取り組まれている問題に加え、着うたやiPod/iTunesなど音楽配信市場が拡大している現在、膨大な楽曲の中から所望の楽曲を得ることを目的とした音楽への自動タグ付けなどが求められています。音楽音響信号のピッチ推定はそういった問題を解決するための一つの手法ですが、楽曲の多様性や音色の豊かさなどから未だ有効な解決策が打ち出されていません。
Specmurt分析は我々が2003年に提案した「ピッチ可視化」を行う手法です。この手法は調波構造が短時間フレーム内でピッチに依存しない(共通調波構造)という仮定をおくことにより、「ピッチの推定」を行う手法に比べシンプルな実装と高速な処理を達成しています。また、共通調波構造を反復推定によって求め、初期値依存性を大幅に低減する手法を開発しました。
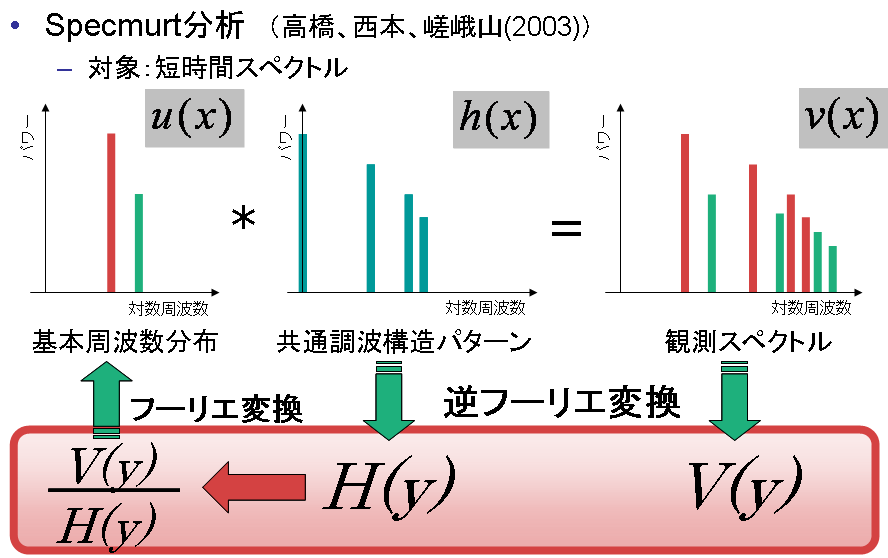
【着眼】楽音の基本周波数と倍音の位置関係は、線形周波数軸上では線形伸縮の関係ですが、これは対数周波数軸上では線形シフトの関係です。もし同時に鳴るいくつかの楽音の倍音の強度比が一定であれば、その観測スペクトルは基本周波数の分布と共通調波構造の畳み込みモデル(線形システム)で記述することが出来ます。
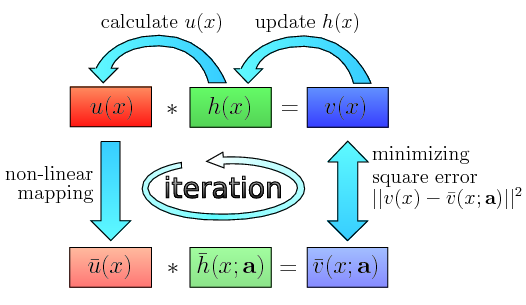
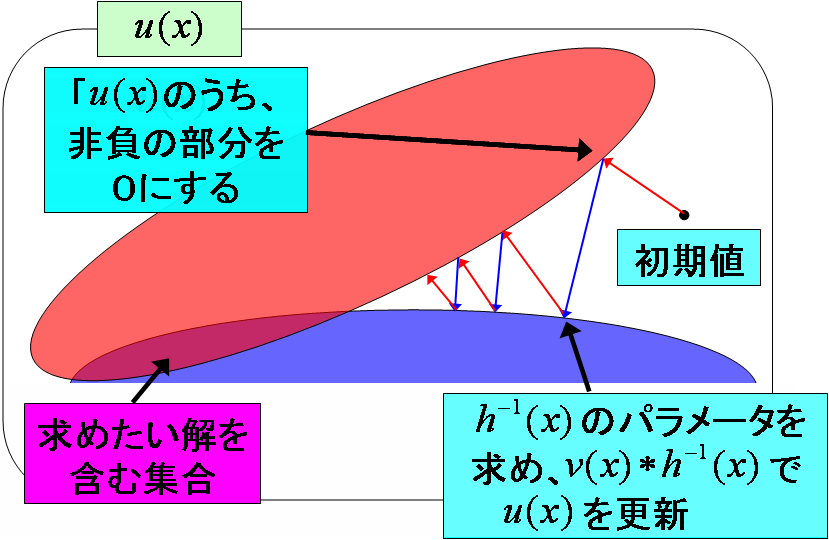
【手法】畳み込みモデルの基本周波数分布は、観測スペクトルと共通調波構造パターンについて、フーリエ変換領域での除算を行い、それを逆フーリエ変換によって元の領域に戻すことによって求められます(図1)。ここで共通調波構造パターンを既知であるとして与える必要がありますが、私たちは非線形写像を用いた反復推定法(図2)、凸射影法を用いた反復推定法(図3)、事後確率最大化Specmurt分析による反復推定法(図4)等の反復的な推定手法を用いることで、初期値として与える共通超は構造パターン依存しにくい頑健推定を実現しました。
【特徴】この手法の特徴は、多重音の生成過程に線形モデルを仮定することにより、他手法よりもシンプルかつ高速な推定が可能であること、また各時刻で特定ピッチが存在する/しないという0/1値だけではなく、連続的な「ピッチらしさ」を時間周波数平面での連続値分布として出力することで、ピッチの「可視化」が可能であることです。
 |
 |
 |
 |
|---|---|---|---|
| 図1. Specmurt分析の概略図。 | 図2. 非線形写像を用いた反復推定により共通調波構造を推定するアルゴリズム | 図3. 凸射影法を用いたアルゴリズムイメージ。凸集合への射影を交互に繰り返すことにより収束が保証される | 図4. 事後確率最大化としてSpecmurt分析を定式化すると、3つの対数確率の和を最大化する問題となる |
キーワード: Specmurt分析、多重ピッチ推定、反復推定法、事後確率最大化
| Title | Composer /arranger |
Genre | Instrument | MIDI conversion pitch accuracy(%) |
|
|---|---|---|---|---|---|
| Non-linear Mapping | MAP Estimation | ||||
| Nocturne No.2 in E flat, op.9-2 | F. Chopin | Classic | Piano | 57.0 | 58.8 |
| For two (Guitar solo) | H. Chubachi | Jazz | Guitar | 68.1 | 65.5 |
| Jive (Piano solo) | M. Nakamura | Jazz | Piano | 59.0 | 60.7 |
| Jive (Guitar solo) | H. Chubachi | Jazz | Guitar | 51.3 | 53.0 |
| Crescent Serenade (Guitar solo) | S. Yamamoto | Jazz | Guitar | 77.5 | 73.1 |