


�$B Noisy Speech Recogniton Using
�$B>e$X�(B: Complex Spectrum Circle Centroid
�$BLa$k�(B: Theoretical Properties of CSCC
It is obvious that the target signal spectrum 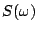 is restored by
finding the centroid of the circle on which three or more microphone
inputs
is restored by
finding the centroid of the circle on which three or more microphone
inputs
 lie. In the case of
lie. In the case of 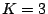 , the circle centroid is
uniquely determined from three distinct points on the circle. In the
case of
, the circle centroid is
uniquely determined from three distinct points on the circle. In the
case of 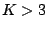 microphone inputs, the circle centroid can be determined
as a point of nearly equal distance from observed microphone inputs. We
estimate the centroid as a point
microphone inputs, the circle centroid can be determined
as a point of nearly equal distance from observed microphone inputs. We
estimate the centroid as a point
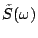 by minimizing
the variance of
by minimizing
the variance of 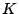 squared distances from
squared distances from
 , i.e.,
, i.e.,
![$\displaystyle \tilde{S}(\omega )=\mathop{\rm argmin}_{Z(\omega)} {\rm\mathop{\mathrm{Var}}\nolimits }
\Big[\Vert Z(\omega)-M_i(\omega) \Vert^2\Big]$](img22.png) |
|
|
(3) |
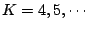 where
where 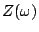 is a point on the complex spectrum
plane for arbitrary. We can include cases of
is a point on the complex spectrum
plane for arbitrary. We can include cases of 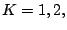 or
or 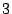 where the
minimum variance is 0.
where the
minimum variance is 0.
To solve this equation, let 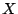 and
and 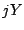 be real and imaginary parts of
be real and imaginary parts of
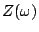 , i.e.,
, i.e., 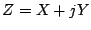 , and let
, and let 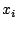 and
and  be those of
be those of
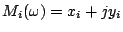 . Then, we have
. Then, we have
from which its partial differentials in respect to 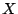 and
and 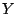 is
derived as:
is
derived as:
denoting the covariance of 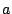 and
and 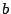 by
by
![$ \mathop{\mathrm{Cov}}\nolimits [a,b]$](img45.png) .
Letting the lefthand side of the above equation be 0, we obtain a linear
equation to obtain the centroid that minimizes the variance of squared
distances in Eq. (3):
.
Letting the lefthand side of the above equation be 0, we obtain a linear
equation to obtain the centroid that minimizes the variance of squared
distances in Eq. (3):
![$\displaystyle \begin{pmatrix}\! X \! [1ex] \! Y \! \end{pmatrix} \!=\! \frac{...
... [y_i,y_i^2] \!\!+\!\! \mathop{\mathrm{Cov}}\nolimits [y_i,x_i^2] \end{pmatrix}$](img46.png) |
(6) |
whose solutions 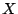 and
and 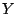 give the estimated complex spectrum centroid
for each frequency as
give the estimated complex spectrum centroid
for each frequency as
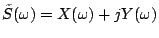 .
.
Eq. (6) has a solution if the covariance matrix:
![$\displaystyle C_{xy}\equiv \frac{1}{2} \begin{pmatrix}\mathop{\mathrm{Var}}\nol...
...m{Cov}}\nolimits [x_i,y_i] & \mathop{\mathrm{Var}}\nolimits [y_i] \end{pmatrix}$](img48.png) |
(7) |
between 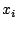 and
and  is regular.
Since its determinant is given by
is regular.
Since its determinant is given by
![$\displaystyle \vert C_{xy} \vert =\mathop{\mathrm{Var}}\nolimits [x_i]\mathop{\...
...sqrt{\mathop{\mathrm{Var}}\nolimits [x_i]\mathop{\mathrm{Var}}\nolimits [y_i]}}$](img50.png) |
(8) |
where 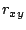 is the correlation coefficient between
is the correlation coefficient between 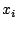 and
and  ,
the solution of Eq. (6) is guaranteed to exist unless
,
the solution of Eq. (6) is guaranteed to exist unless
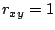 , i.e., all spectrum points
, i.e., all spectrum points
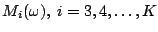 lie on a line in the complex plane.
lie on a line in the complex plane.
Even though 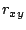 is always guaranteed to be no greater than 1, in
numerically bad conditions such as
is always guaranteed to be no greater than 1, in
numerically bad conditions such as
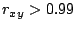 , we use the center of
gravity of
, we use the center of
gravity of 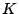 points
points
 , i.e., the delay-and-sum solution,
instead of the circle centroid here.
, i.e., the delay-and-sum solution,
instead of the circle centroid here.



�$B Noisy Speech Recogniton Using
�$B>e$X�(B: Complex Spectrum Circle Centroid
�$BLa$k�(B: Theoretical Properties of CSCC
�$BJ?@.�(B16�$BG/�(B9�$B7n�(B23�$BF|�(B
![]() is restored by
finding the centroid of the circle on which three or more microphone
inputs
is restored by
finding the centroid of the circle on which three or more microphone
inputs
![]() lie. In the case of
lie. In the case of ![]() , the circle centroid is
uniquely determined from three distinct points on the circle. In the
case of
, the circle centroid is
uniquely determined from three distinct points on the circle. In the
case of ![]() microphone inputs, the circle centroid can be determined
as a point of nearly equal distance from observed microphone inputs. We
estimate the centroid as a point
microphone inputs, the circle centroid can be determined
as a point of nearly equal distance from observed microphone inputs. We
estimate the centroid as a point
![]() by minimizing
the variance of
by minimizing
the variance of ![]() squared distances from
squared distances from
![]() , i.e.,
, i.e.,
![]() and
and ![]() be real and imaginary parts of
be real and imaginary parts of
![]() , i.e.,
, i.e., ![]() , and let
, and let ![]() and
and ![]() be those of
be those of
![]() . Then, we have
. Then, we have 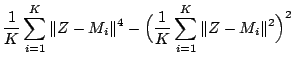
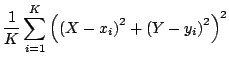
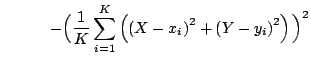
![$\displaystyle C_{xy}\equiv \frac{1}{2} \begin{pmatrix}\mathop{\mathrm{Var}}\nol...
...m{Cov}}\nolimits [x_i,y_i] & \mathop{\mathrm{Var}}\nolimits [y_i] \end{pmatrix}$](img48.png)
![]() is always guaranteed to be no greater than 1, in
numerically bad conditions such as
is always guaranteed to be no greater than 1, in
numerically bad conditions such as
![]() , we use the center of
gravity of
, we use the center of
gravity of ![]() points
points
![]() , i.e., the delay-and-sum solution,
instead of the circle centroid here.
, i.e., the delay-and-sum solution,
instead of the circle centroid here.