一方、我々は音声認識で多用される学習アルゴリズムをヒントにして、
ウェーブレット変換などで求めたパワースペクトル分布![]() (
(![]() は対数周波数)
は多数のwaveletの標本分布であると解釈し、広がって分布する周波数成分をク
ラスタ化する視点から、高精度な多重ピッチ推定手法[39,40]
を提案した。
は対数周波数)
は多数のwaveletの標本分布であると解釈し、広がって分布する周波数成分をク
ラスタ化する視点から、高精度な多重ピッチ推定手法[39,40]
を提案した。
各重心が調波関係にある複数のクラスタからなる結びクラスタを複数個用意し、 この結びクラスタの重心を求める。これは、高調波成分をすべて基本周波数成分 に集約させ、あたかも純音のスペクトルと見なして基本周波数を推定することと 同等になる。Specmurt 法などで求めた初期値から出発して、繰り返し演算によ り、このような調波関係拘束条件下でのクラスタリングアルゴリズムにより高精 度な多重ピッチを推定する手法をHarmonic Clusteringと呼ぶ。
スペクトル密度![]() と
第
と
第![]() クラスタの
クラスタの![]() 倍音
倍音![]() に帰属する確率
に帰属する確率
![]() との積は、クラスタ
との積は、クラスタ![]() に割り当てられた標本値
に割り当てられた標本値![]() の標本数
と考えることができる。従って、
の標本数
と考えることができる。従って、
![]() 番目の結びクラスタのうちの基本周波数推
定値に相当するクラスタ重心を
番目の結びクラスタのうちの基本周波数推
定値に相当するクラスタ重心を![]() とすると、帰属する標本数にクラスタ重
心までの距離関数
とすると、帰属する標本数にクラスタ重
心までの距離関数
![]() (通常は正規分布形状を使用)を乗
じて積分したクラスタリングの目的関数は
(通常は正規分布形状を使用)を乗
じて積分したクラスタリングの目的関数は
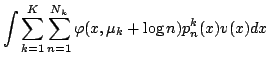 |
(9) |
結びクラスタの数は同時発音数に相当するが、適切な結びクラスタ数(パラメー タ数に直結)をAICなどの情報量規準を用いて推定することができる [40]。また、ピッチ推定研究において永年の課題であった倍ピッチ/ 半ピッチ誤りを回避して適切な基本周波数を見つける問題も同様に情報量規準の 問題に帰着させることができる[40]。