等方的雑音場を直交化するアレイ信号処理の理論と
パワースペクトル推定への応用

小野順貴

松本恭輔

嵯峨山茂樹

研究の概要

【背景】雑音環境における雑音抑圧に関しては代表的な手法としてSpectral Subtraction, Delay-and-Sum Array(Beamforming), 死角型アレー(Null-Beamforming)などが挙げられます。しかし, これらの手法では"雑音信号のみを観測する必要がある", "実用的なアレイサイズでは十分な雑音抑圧が達成されない", "(マイクロフォンの個数 - 1)方向の雑音までしか抑圧できない"といった問題点があります。

【目的】本研究では音声認識への応用を推定し, "周囲のあらゆる方向から雑音が到来する環境で","雑音のみを観測することなく", "実用的なアレイサイズで", 既知方向から到来する単一目的信号のパワースペクトルを取得することを目的とします。

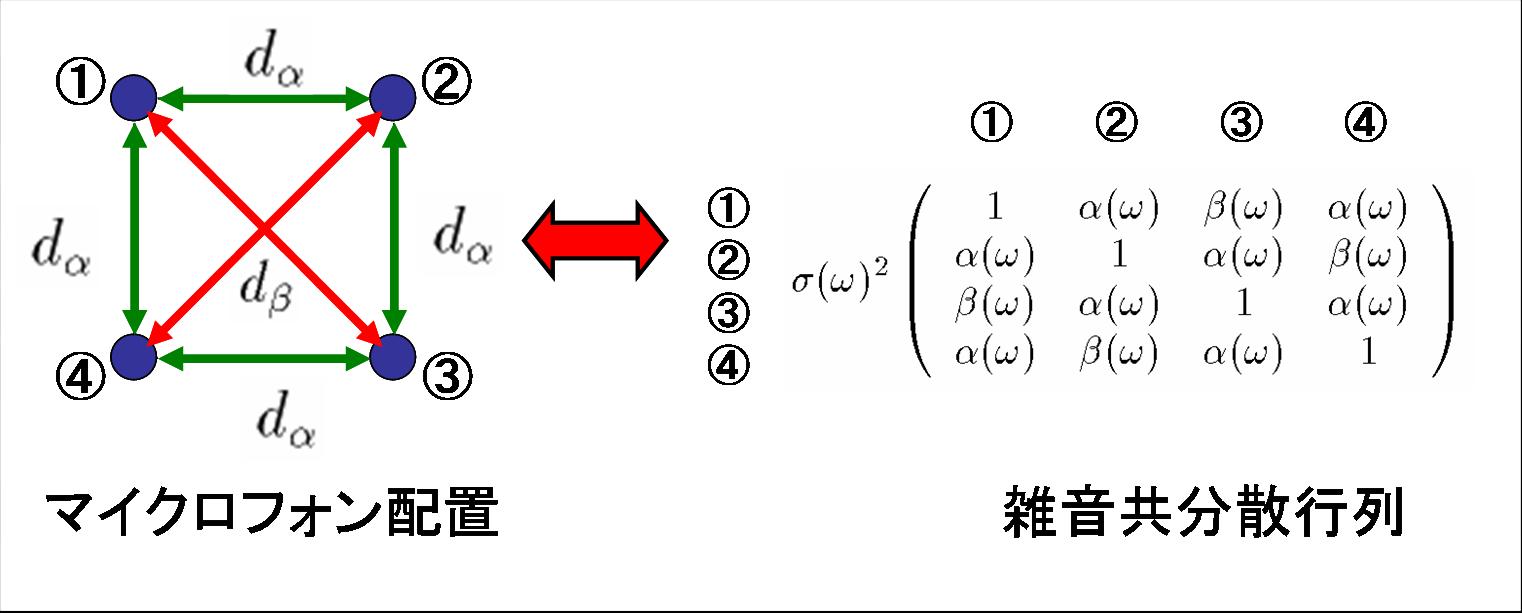
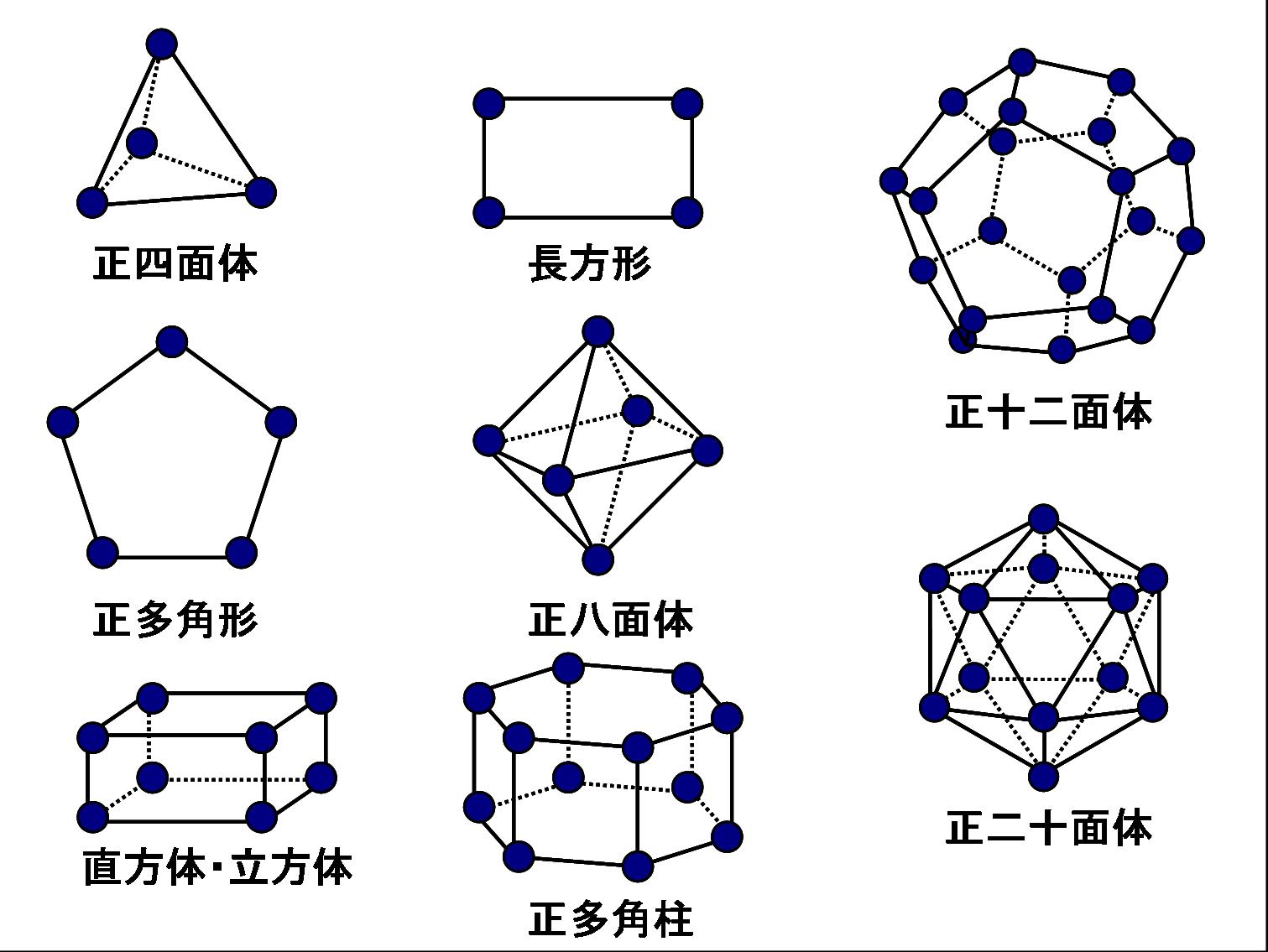
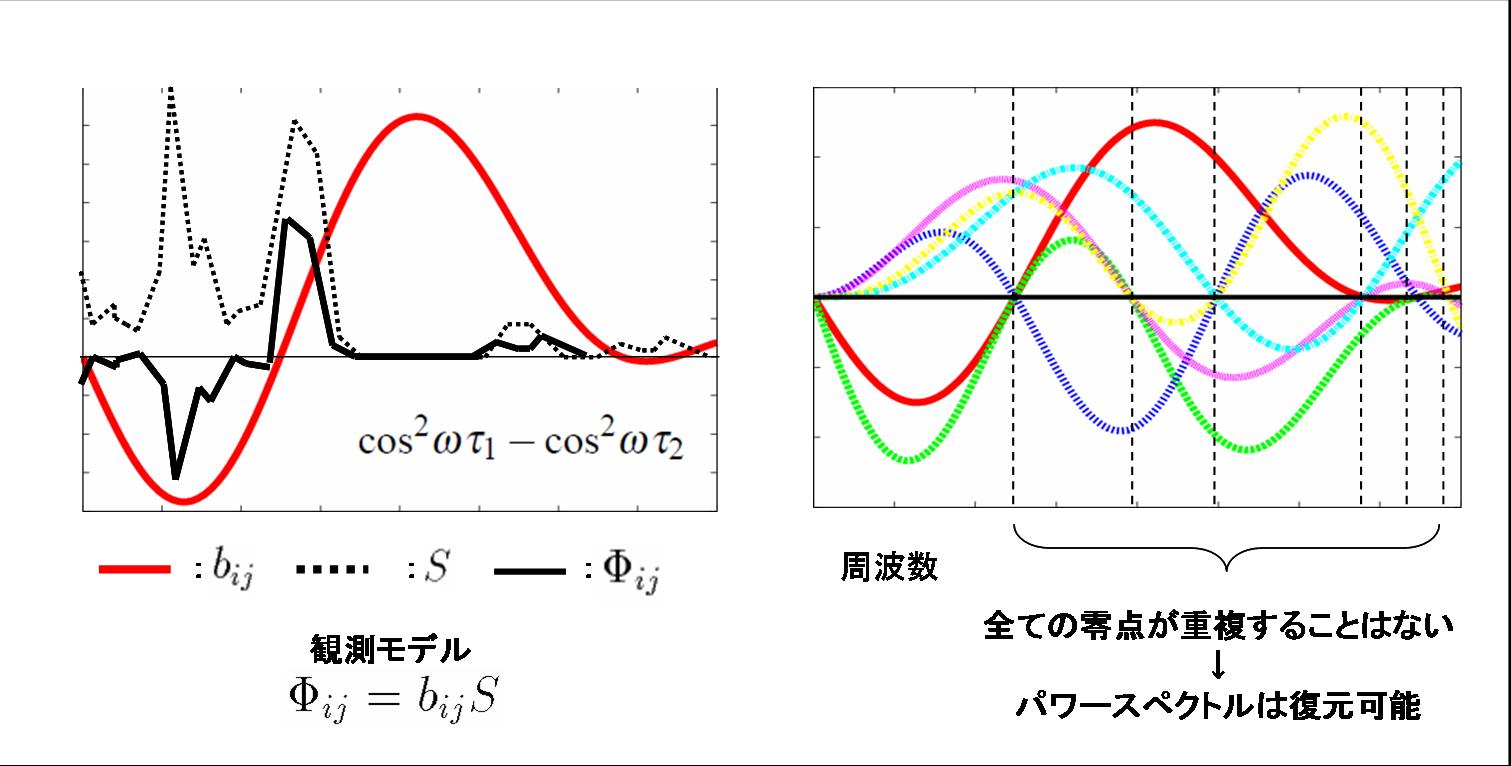
【手法】上述のような雑音場として等方的雑音場を定義すると, 観測信号の共分散行列は例えば図1のように表されます。本手法ではこの共分散行列を対角化することによりノイズフリークロススペクトルを取得し, これを利用して元のパワースペクトルを復元します。本研究では図2に示されるセンサ配置であれば, 共分散行列の具体的な値を求めずとも, ある同一のユニタリ行列で対角化することが可能であることを示しました。観測されるクロススペクトルは, 図3で示されるようにパワースペクトルをフィルタリングしたものとモデル化することができ, この逆フィルタを求めることでパワースペクトルが復元できます。

【特徴】本手法は対称的なアレイ配置という計測一般に通用するアイデアに基づいており, 音響信号処理では残響場への応用などが期待されます。

図1. 正方形の頂点にマイクロフォンを配置した場合の雑音共分散行列。	図2. 提案手法を可能とするセンサ配置	図3. パワースペクトルと観測されるクロススペクトルの関係

キーワード: 等方的雑音場, 対称性, 直交化, クロススペクトル, スペクトル推定

関連文献

[Shimizu2007ASJ03]においてシミュレーション実験に基づく本研究の成果が報告されました。

• [Shimizu2007ASJ03]
  清水 光, 小野 順貴, 松本 恭輔, 嵯峨山 茂樹, "等方的雑音場を直交化するアレイ信号処理の理論とパワースペクトル推定への応用," 日本音響学会春季研究発表会講演集, Mar. 2007. [PDF file]

シミュレーション実験による評価

• マイクロフォンの周囲から雑音を加えて仮想的な等方的雑音場をつくります。雑音場の種類として
  1, 等しいパワーの白色雑音(波形は異なる)を64方向から加える
  2, 相異なる50の音声を10方向から加える(同一方向からは5個の音声の重ね合わせ)
  の2種類で実験します。2の実験条件ではより実環境に近い雑音場であると考えられます。
• 推定されたパワースペクトルの推定精度を評価する関数としてSD(Spectral Distortion Measure)という一般的な評価関数を用います。元の観測信号のSN比[dB]を変化させた時のSD[dB]の変化を評価します。
• 同一の個数のマイクロフォンを用いたSpectral DistortionとDelay-and-Sumを比較対象をします。Spectral Distortionでは観測時間内の雑音のパワースペクトルの平均を与えます。Delay-and-Sumに関しては各マイクロフォンの観測信号に位相補償をかけるという基本的な処理を施します。

図4. SDによる評価です。左が実験条件1, 右が実験条件2による結果です。両実験結果とも提案手法の推定精度が最も良いことを示しています。	図5. 推定されたパワースペクトルです。赤が真値, 水色が提案手法, その他の色は比較対象の手法を示しています。雑音のパワーよりもはるかに小さい目的信号のパワーが提案手法によってのみ復元されています。	図6. スペクトログラムによる推定精度の評価です。横軸が時間, 縦軸が周波数, 色の度合がパワーの大きさを表します。提案手法の推定精度が最も良いことが視覚的に確認されます。