Isotropic Noise Field Orthogonalization in Array Signal Processing
and its Application to Power Spectrum Estimation

Hikaru Shimizu

Nobutaka Ono

Kyosuke Matsumoto

Shigeki Sagayama

Abstract

[Motivation] There exist several effective noise suppression methods for noisy environments such as spectral subtraction, beamformer (Delay-and-Sum array), and null beamformer, but these methods suffer from severe limitations. Spectral subtraction needs to be able to observe only noise, while the D-S beamformer requires impractical array size for adequate separation performance, and the null beamformer can suppress noise coming from only up to (number of microphones -1) directions

[Focus] In this research, we aim at developing a noise suppression method to be applied to speech recognition, and thus need to be able to estimate the power spectrum of one target signal from a given direction in a noisy environment where noise is arriving from all directions, without the necessity to observe noise separately, while keeping a pratical array size.

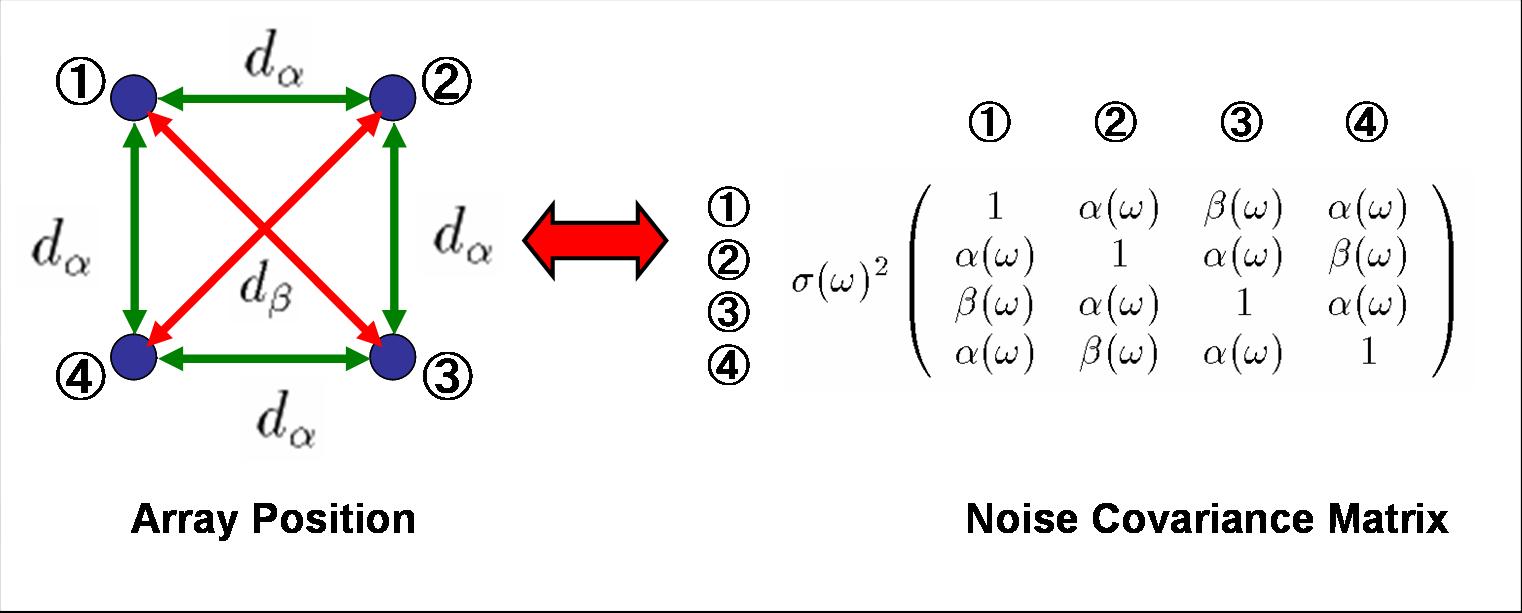
[Method] As an idealization of a noise field in which noise arrives from all directions, we define the Isotropic Noise Field. In an Isotropic Noise Field, the noise covariance matrix is expressed as in Fig. 1. We proposed a new spectrum estimation method, in which we estimate the power spectrum using the noise-free cross-spectrum acquired by orthogonalization of the noise field. 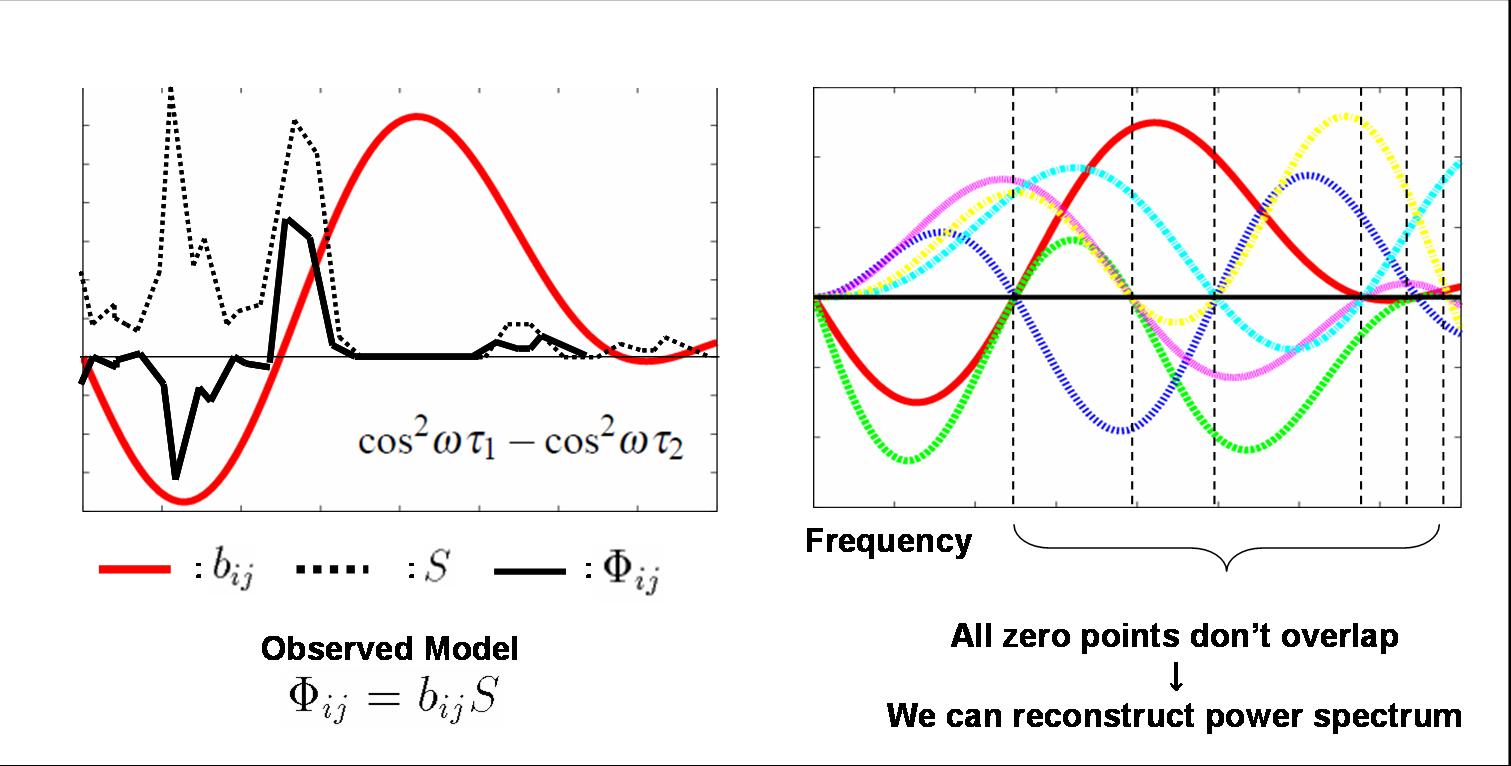In this research, we proved that the noise covariance matrix of an Isotropic Noise Field is diagonalized by the same unitary matrix independently of the discrete values of the matrix, when the position of the microphones in the array is set as shown in Fig. 3. The observed cross-spectrum is modeled as a filtered version of the power spectrum, and we can reconstruct the power spectrum by estimating the corresponding inverse filter.

[Characteristics] This method is based on a very general idea, the symmetrical setting of the sensor array, which could be used in many areas. In signal processing, we expect this method to be applied effectively to reverberation fields.

Fig. 1. Structure of the observed noise covariance matrix for a square microphone array.	Fig. 2. Sensor positions for which the proposed method can be applied.	Fig. 3. Relation between power spectrum and observed cross-spectrum.

Keywords: Isotropic Noise Field, Symmetry, Orthogonalization, Cross-Spectrum, Spectrum Estimation

Bibliography

This idea and experimental results based on simulation were reported in Japanese [Shimizu2007ASJ03]

• [Shimizu2007ASJ03]
  Hikaru Shimizu, Kyosuke Matsumoto, Nobutaka Ono, Shigeki Sagayama, ``A Theory of Array Signal Processing to Orthogonalize Isotropic Noise Field and its Application to Power Spectrum Estimation,'' Proc. of ASJ Spring Meeting, pp.569-570, Mar., 2007. (in Japanese) [PDF file]

Experimental results based on simulation

• We simulated an Isotropic Noise Field by adding noise from all around the microphone array. We generated 2 kinds of noise field as follows:
  1. Add noise from 64 directions. (each noise has the same power spectrum, but a different waveform in the time domain)
  2. Using 50 different speech signals, add 5 superposed signal from 10 directions.
  Experimental condition 2 is thought to be more practical than 1.
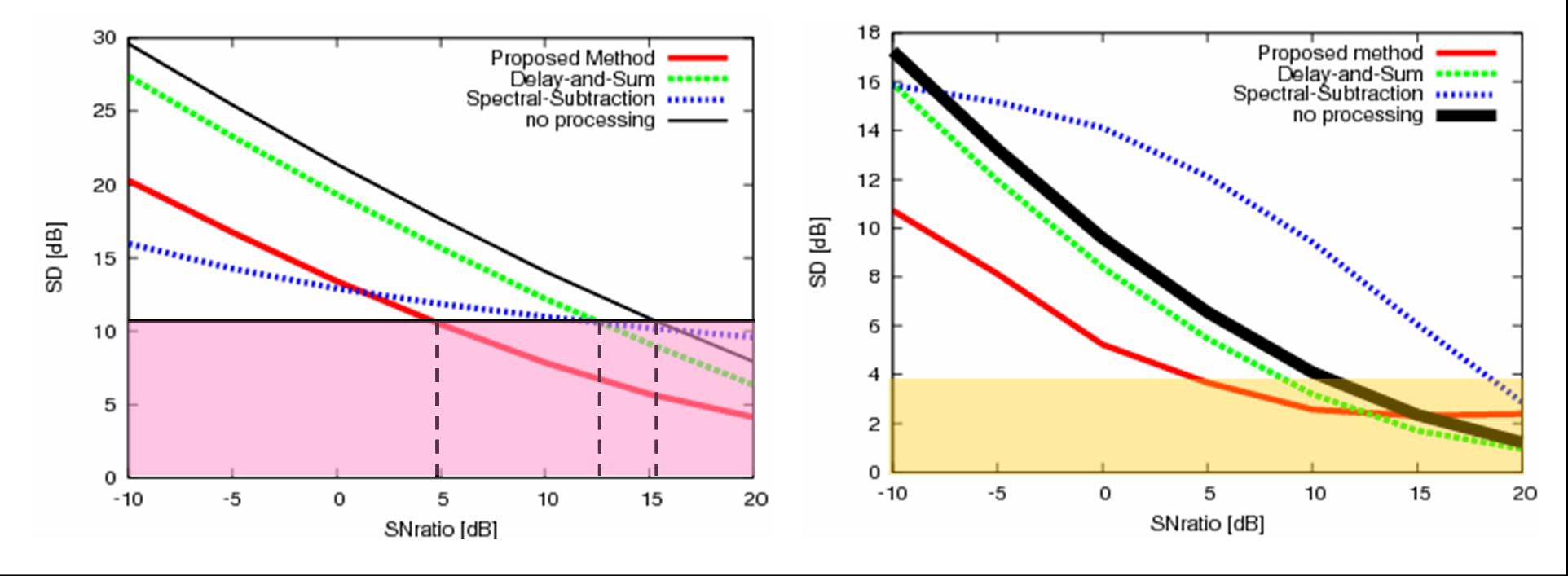
• We use the Spectral Distortion measure (SD) as a general evaluation function for the estimated power spectrum. We evaluate SD for different SN ratios of the observed signal.
• As comparison methods, we use Spectral Subtraction and Beamforming by Delay-and-Sum Array with the same number of microphones. We provide the averaged power spectrum at all observation times for Spectral Subtraction, and use basic phase compensation for the Delay-and-Sum Array.

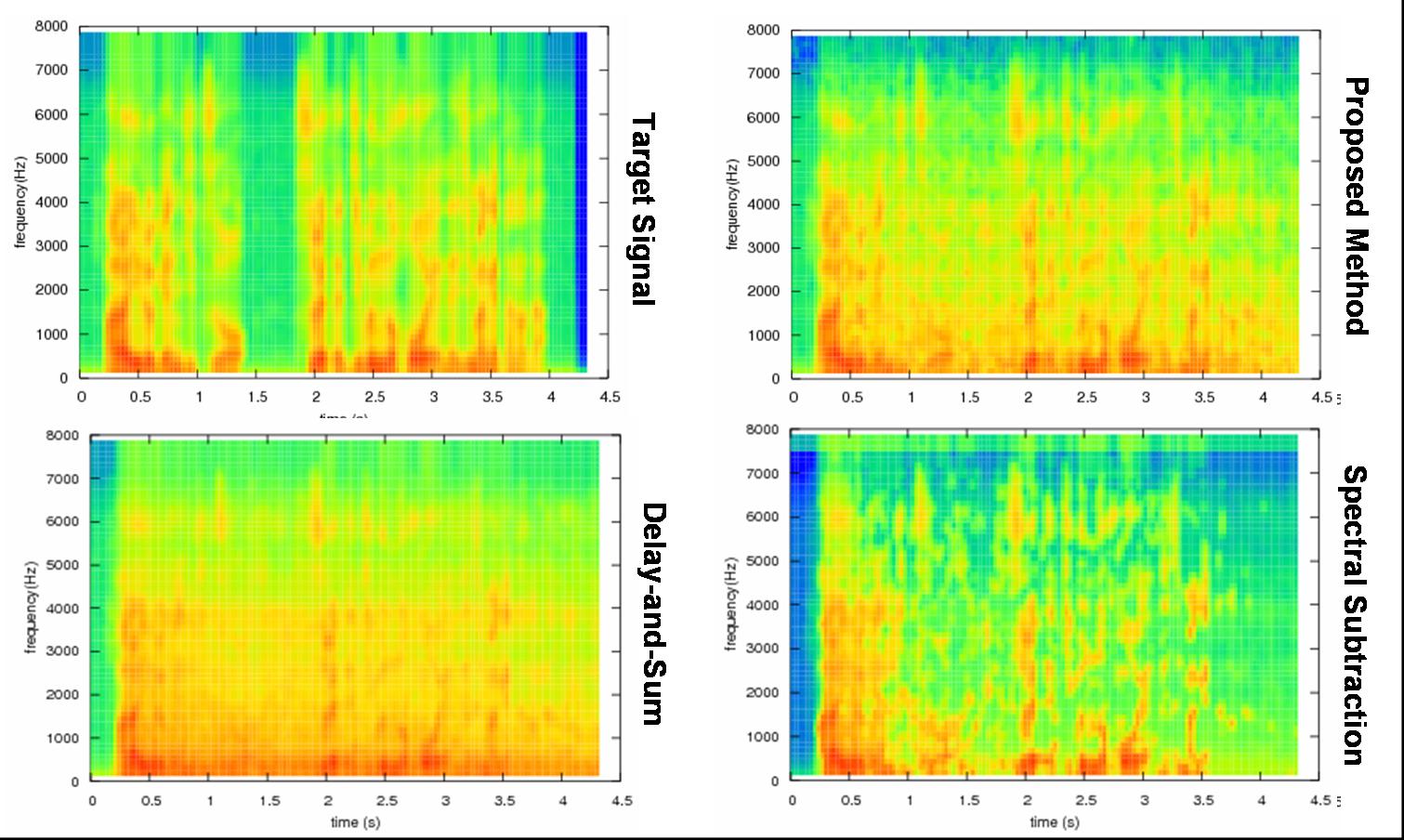
Fig. 4. Evaluation by SD for experimental condition 1 (left) and 2 (right). Both graphs show the effectiveness of the proposed method.	Fig. 5. Estimated power spectrum. The true power spectrum is shown in red, the spectrum estimated by the proposed method in light blue, the observed spectrum in green, the spectra estimated by Delay-and-Sum in dark blue and by Spectral-Subtraction in pink.	Fig. 6. Comparison of estimation accuracy by spectrograms. Horizontal axis represents time, vertical axis represents frequency. These spectrograms also show the effectiveness of the proposed method.